
ベクトル解析 その4 回転 Rot 回転はなぜ回転を表すのか Youtube
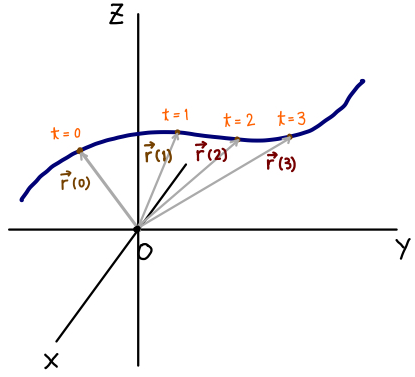
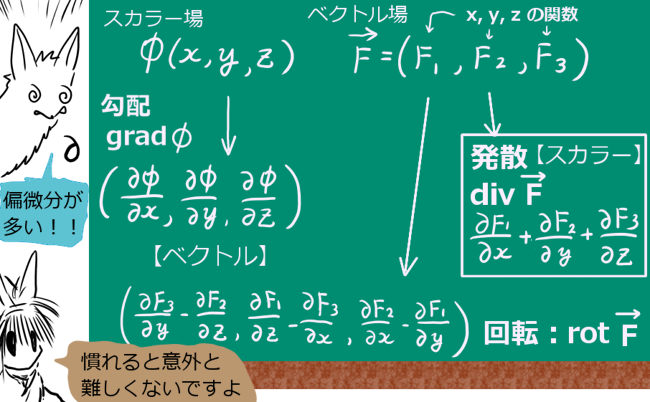
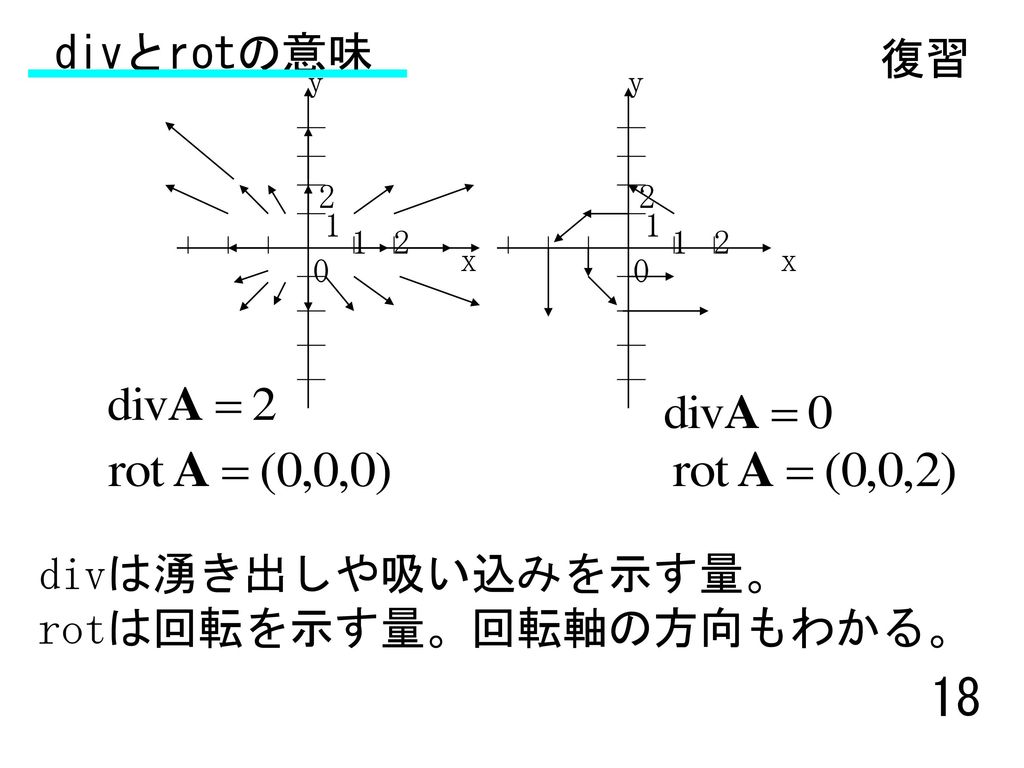
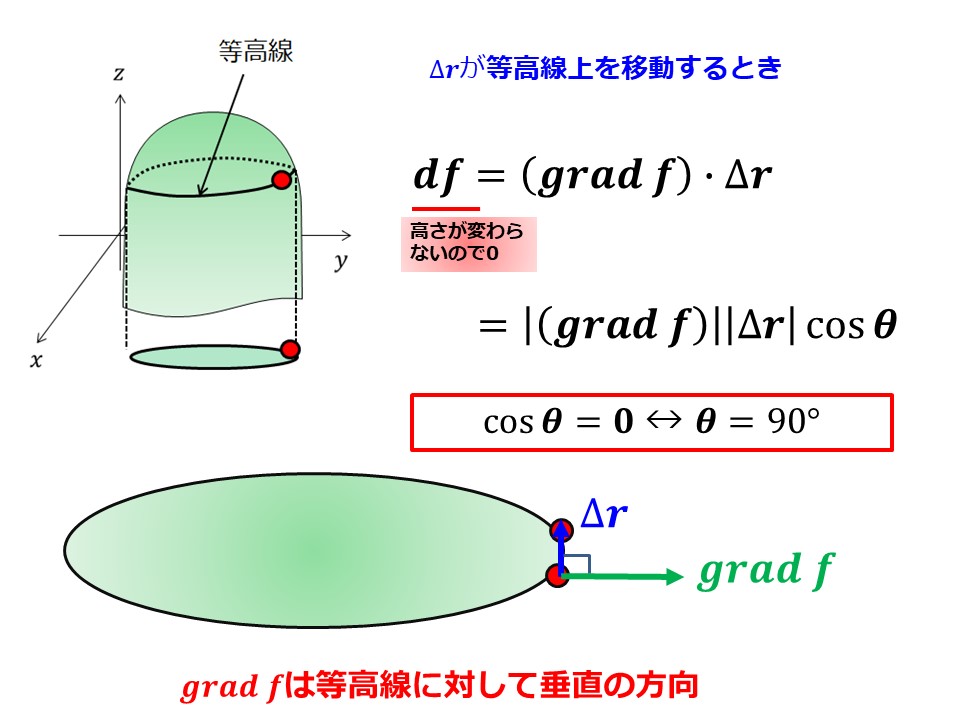
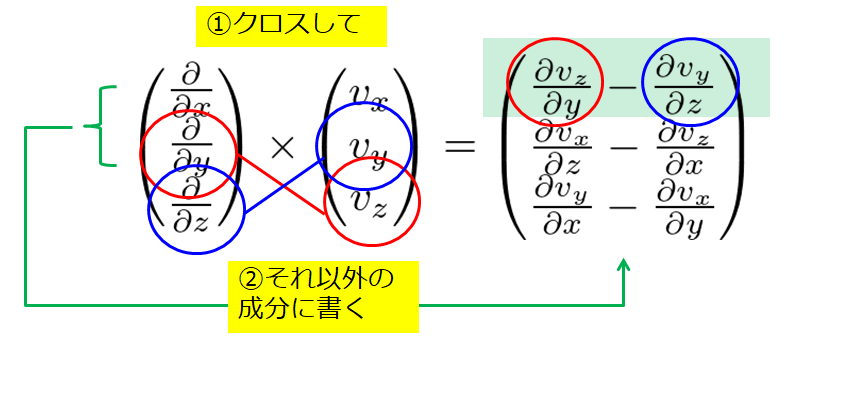
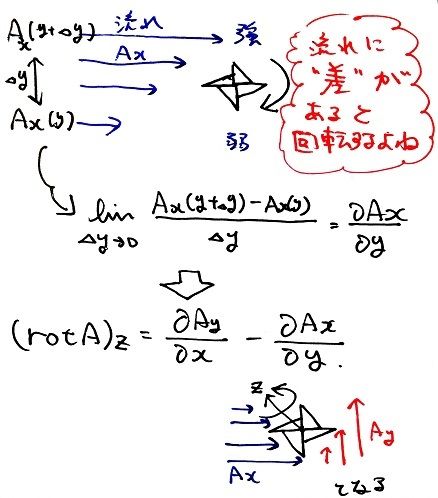
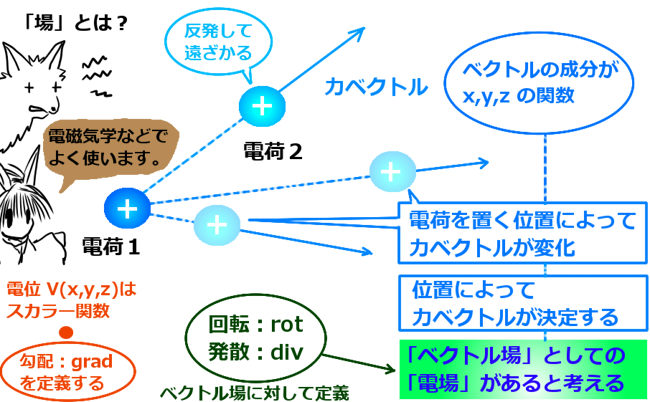
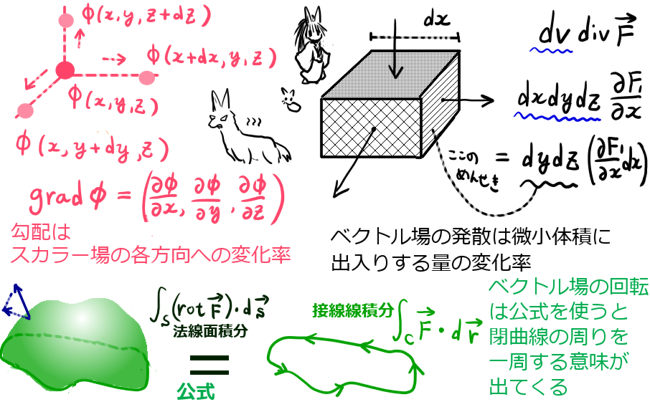
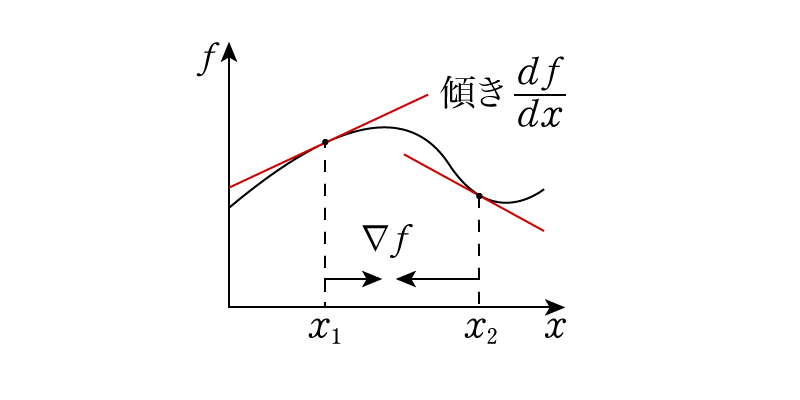
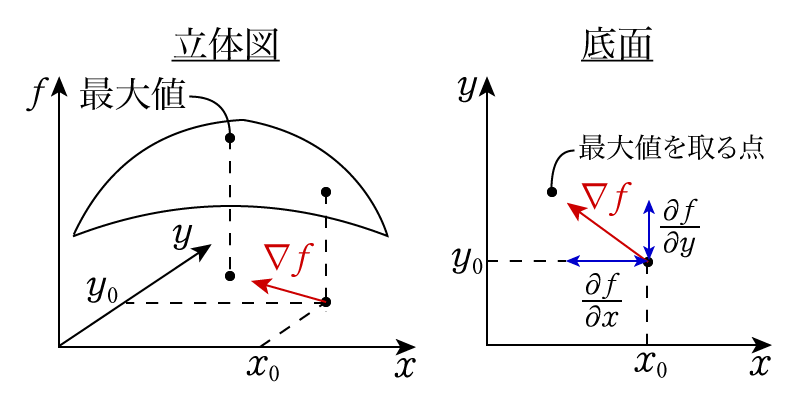
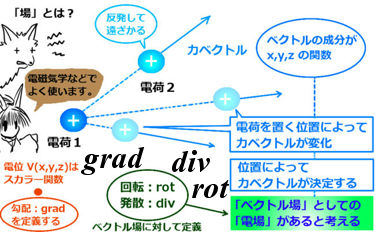
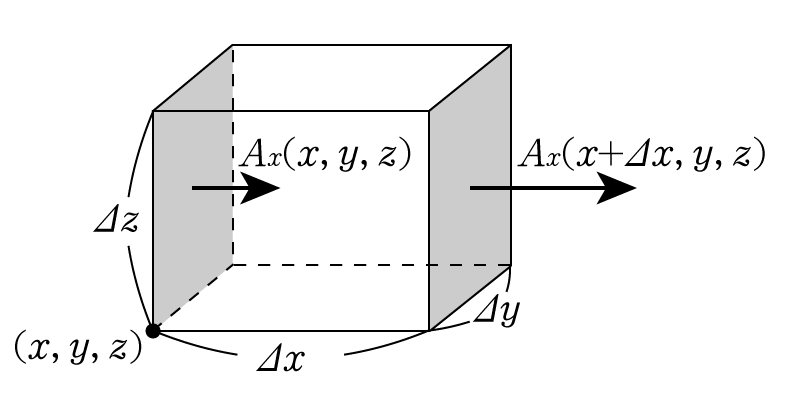
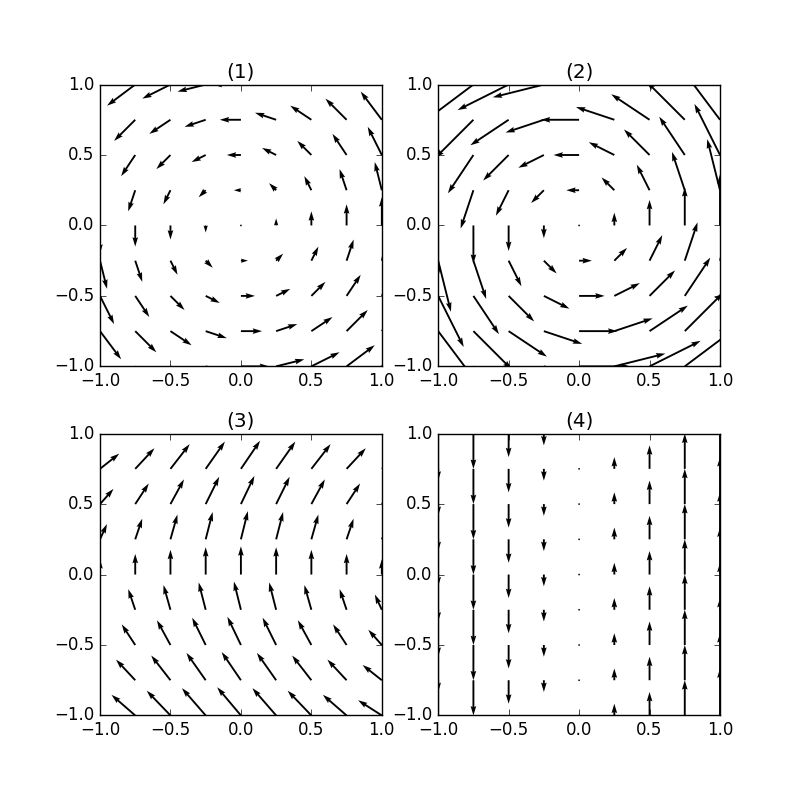
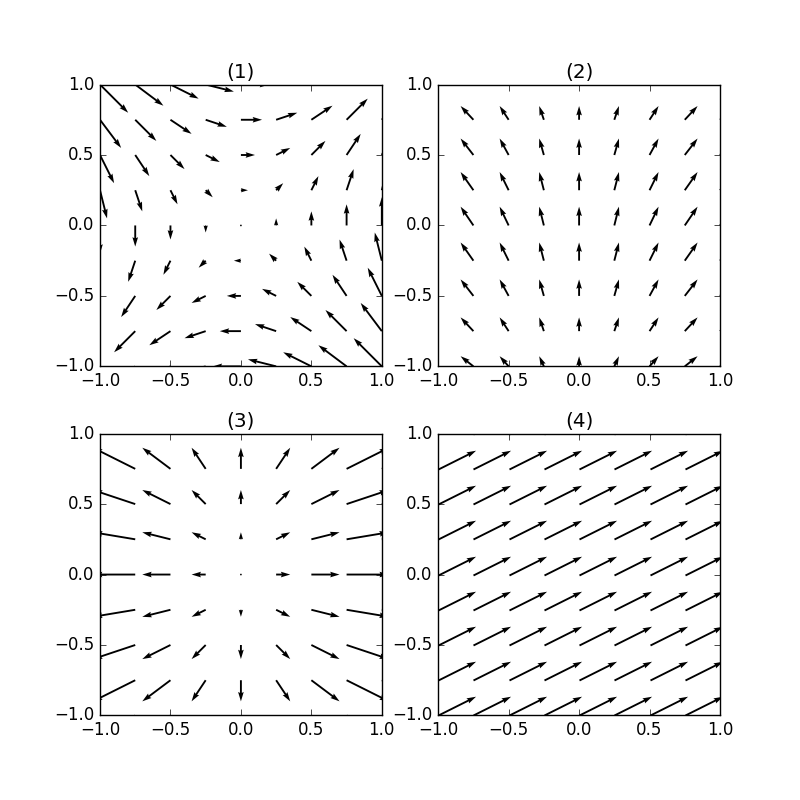
回転 ∇× (rotまたはcurl) 「回転」の定義は以下の通りです。 あるベクトル変数A=(A x, A y, A z)があったとき、Aの回転∇×Aは で表される。 やっていることは外積の計算と同じです。ただ単にa x ,a y, a z が微分演算子になっただけです。ランクはどうなってなぜ,勾配というのか ⇒ 方向微分 (2) div A 発散 divergence といいます。 (3) rot A 回転 rotation といいます。
Rot 回転 なぜ
Rot 回転 なぜ- ベクトル場の回転(rotation)の極座標系による表現を求めるページです。導出には合成関数の微分と極座標系の基底ベクトルを用います。 (なぜなら $0 \leq \theta \leq \pi$) であることを用いた。 同様の計算により、 が示される。 $\phi$ の微分については $(2Rot 2 const m nse J B = (6) である.ここで,この定数が0の場合に超伝導状態の解があると仮定すると, 0 * * rot 2 J B = m nse (7) となり,これはロンドン方程式と呼ばれている. ここで,変位電流の項(∂ D/∂t)を無視した場合のマクスウェル方程式rotB=μ0Jを用い
ベクトルの回転 Rot ベクトル解析 基礎からの数学入門
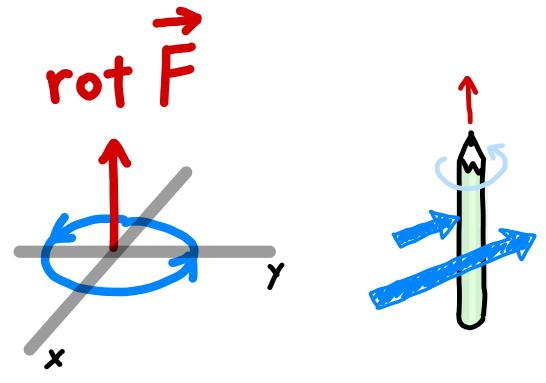
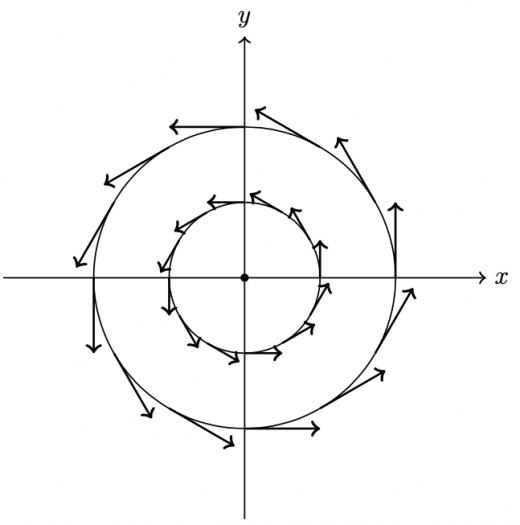
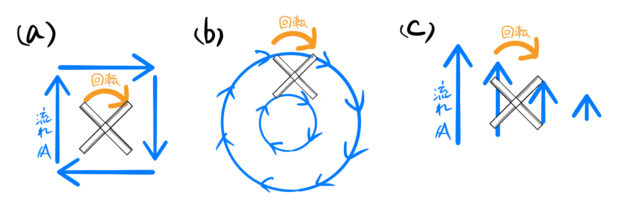
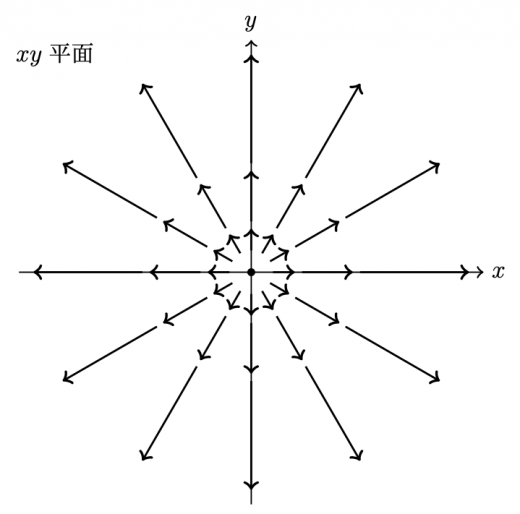
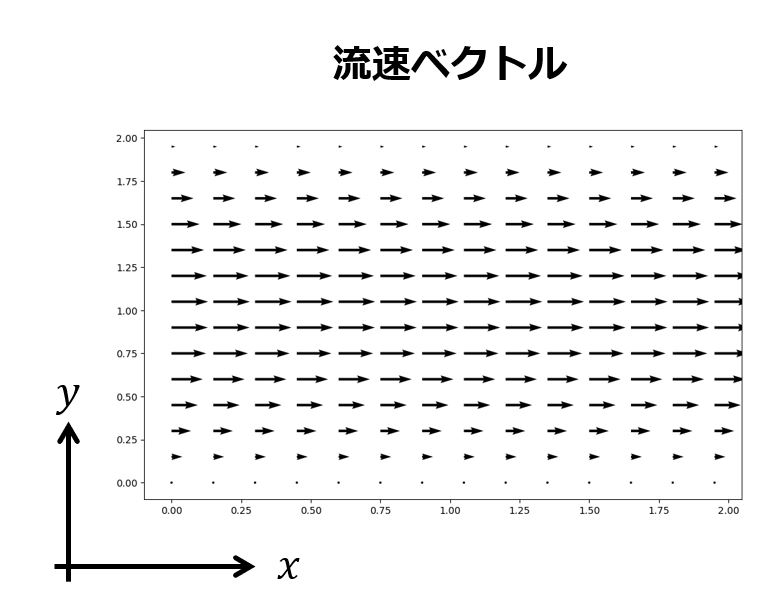
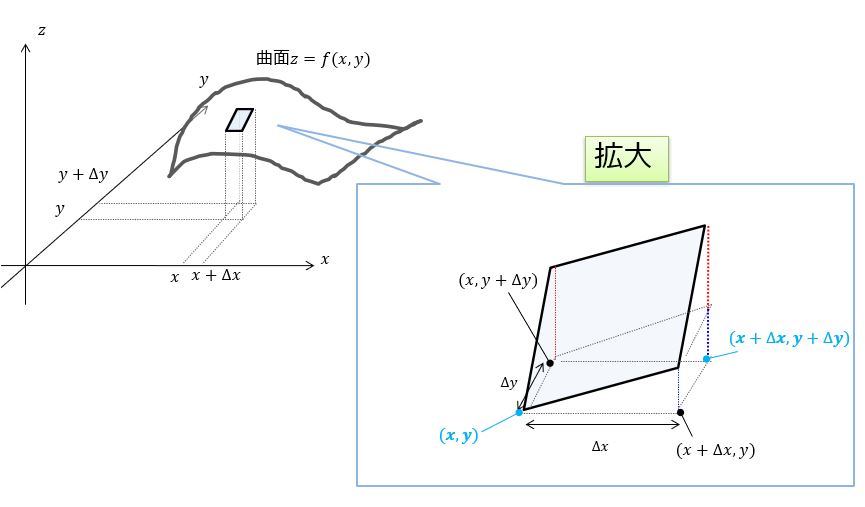
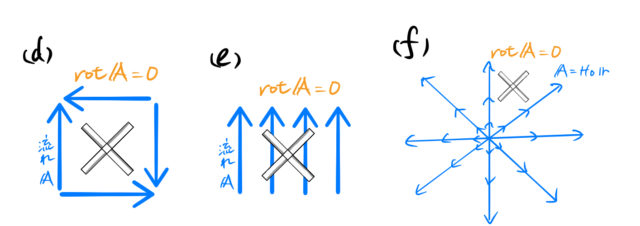
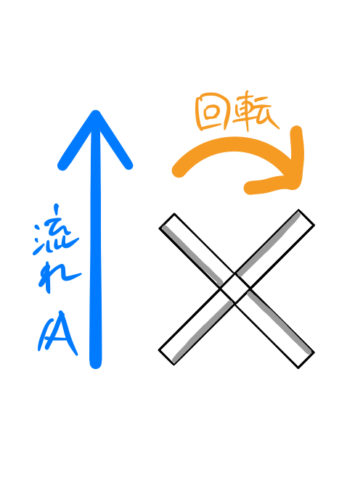
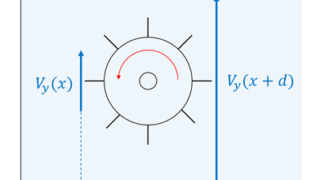
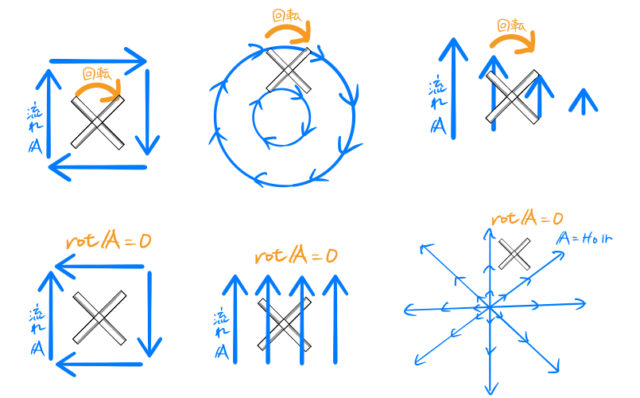
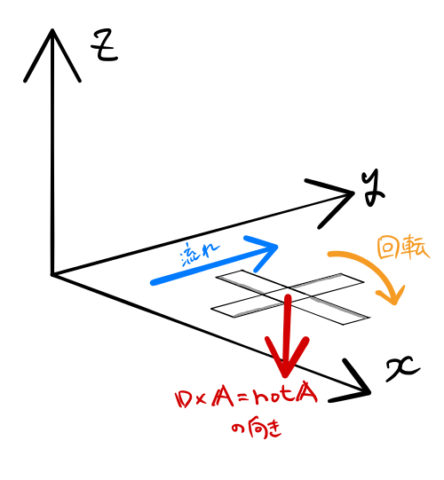
ベクトルの回転(rot)は流れ(ベクトル)に作用する。 ベクトルの矢印の大きさはその場での流れの強さを表している。 流れは風の流れでも良いし水の流れでも良い。 ここでは、風の流れをイメージしてみる。 ベクトルの回転が 0 ではないとはどういうことか? 風の流れをベクトル で表しておく。 図のように立てた風車(かざぐるま)*1は、風の流れベクトル によって回転するだろう。 風車が回面積素とパラメータ (曲面 z=g(x,y) の場合) 曲面 z=g(x,y) の法線;回転行列による実ベクトルの回転(2次元・3次元) 回転行列 (rotation matrix) は,ユークリッド空間上のベクトルとの積を取ることにより,そのベクトルを回転させる演算子(作用素)として働きます.このことを,2次元回転行列および3次元回転行列に関して,三角関数の加法定理を用いて証明します.また,回転行列の転置行列,逆行列,行列式などの性質とその意味を説明します. スマホ
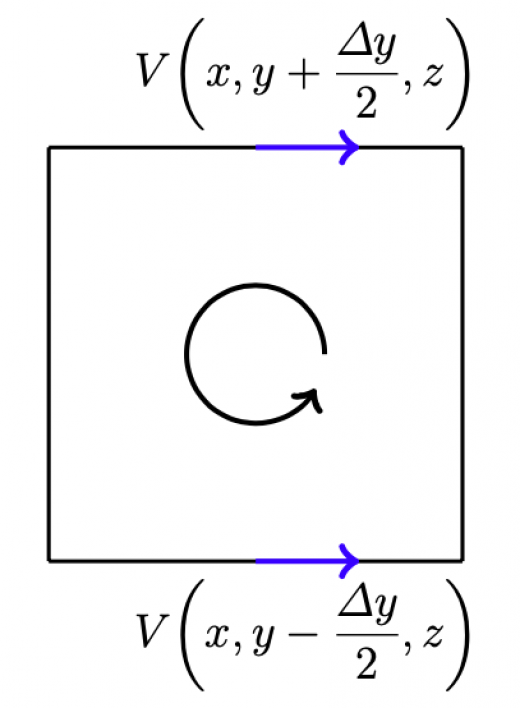
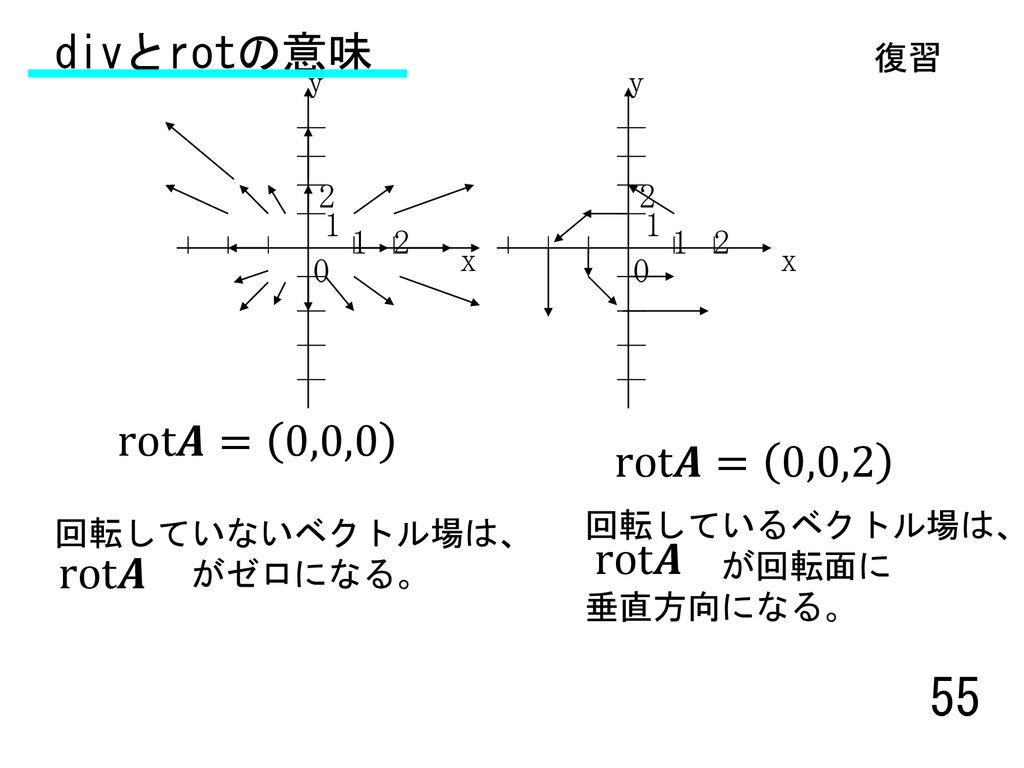
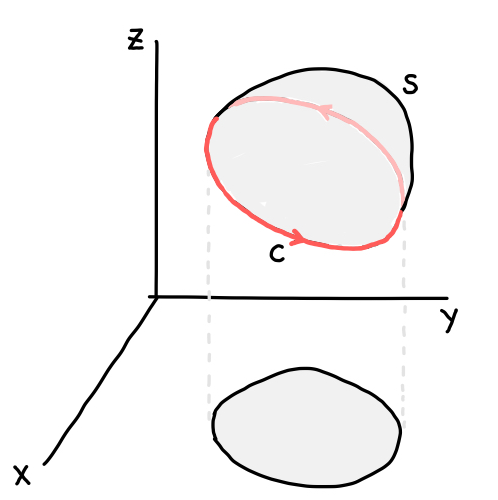
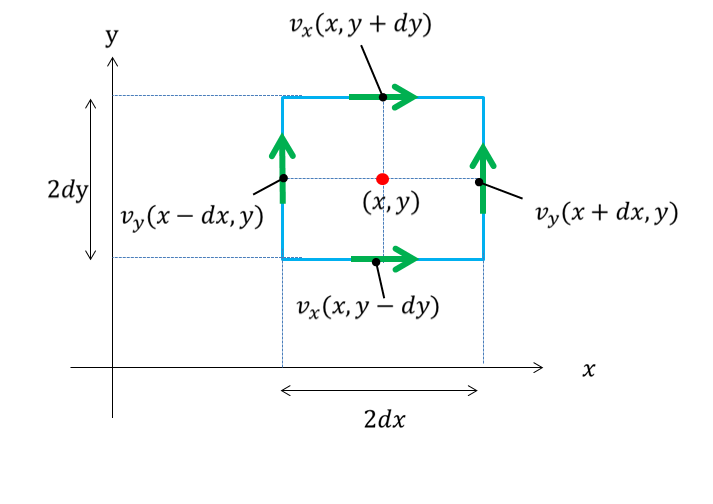
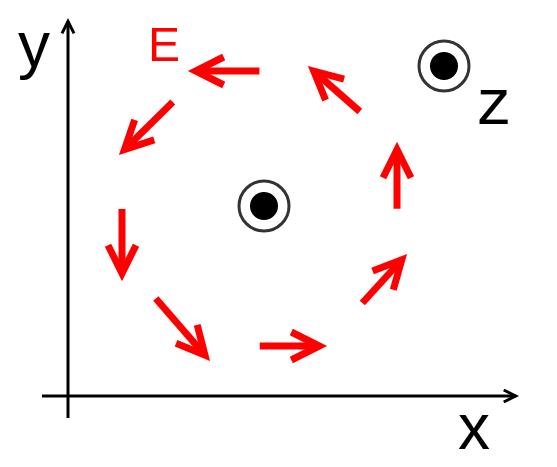
Rot E = 0 静電界では rot E = 0 が成立する。 静電界は保存力の場なので、仕事の周回積分は 0 である。 すなわち、 ∳ F ・d r = 0 が成り立つ。 この経路を微小な正方形の辺にあてはめればよい。 ( 微分なので rot E = 0 と書いても問題ない。 v と表すこともある. このように 勾配 grad は関数 f R n → R に 発散 div はベクトル値関数 v R n → R n に 回転 rot はベクトル値関数 v R 3 → R 3 に 対して定義します. ナブラ (nabla) ∇ を使うと,いまみた3つの微分作用素 grad, div, rot をスッキリ表すことができるのでした. 変数 x = ( x 1, , x n) に関して, ∇ = ∂ 1 ⋮ ∂ n と (形式的に)定め, grad 回転は「ローテーション」とも呼ばれていて、「∇×」とか「rot」とか「curl」といった記号で表されます。 右ねじの法則というものを知っていますか? ねじは「の」の字に回すと材料の奥へ入っていきますよね。 回転という物理的な力を与える(トルクを与える)ことでねじは材料に対して下へ下へ力を与えていきました。 そして、強く回転させるほど強く下に力が加わりました。 回
Rot 回転 なぜのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 | ||
 |  |  |
「Rot 回転 なぜ」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 | ||
「Rot 回転 なぜ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「Rot 回転 なぜ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
「Rot 回転 なぜ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | 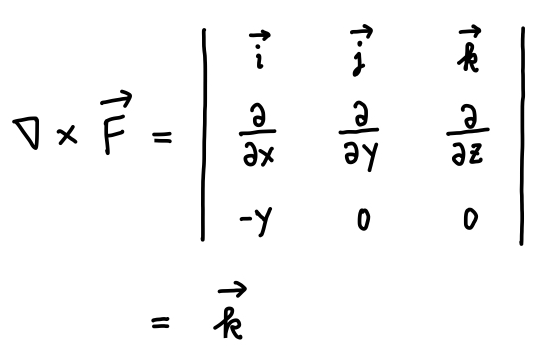 | |
「Rot 回転 なぜ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
「Rot 回転 なぜ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
「Rot 回転 なぜ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「Rot 回転 なぜ」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
「Rot 回転 なぜ」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 | ||
「Rot 回転 なぜ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「Rot 回転 なぜ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |
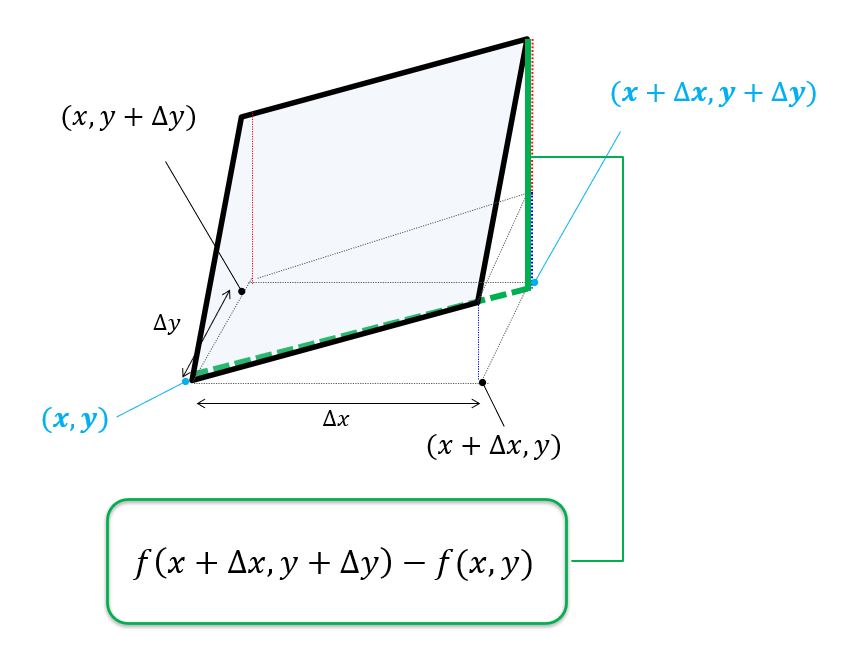
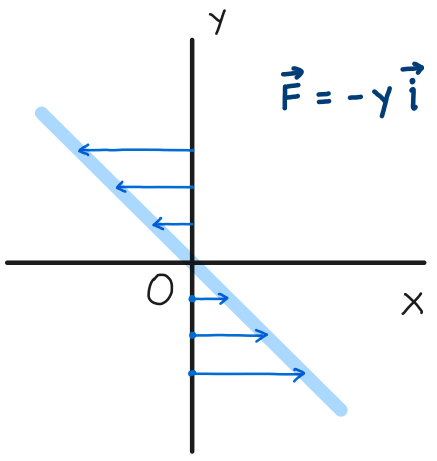
ベクトルの回転 rot (x,y,z)k があるとき、 次のベクトルを 回転 (rotation) といいます。 \text {curl} curl と書くこともありますが、同じ意味です。 「回転」のイメージ。 \overrightarrow {F} F の「回転」が上の式ですよ、と言われても、何かクルクル回ってるわけでもないし、「何でこれが回転なの? 何が回ってるの? 」と疑問に思うのではないでしょうか。 それでは隣接する電場の回転の差が、磁場の時間変化になる。 電場のZ軸方向の変化量と、磁場の時間変化をつないでいるのが 回転のrotというわけなのだ。 視覚的にrotと回転がつながったので まさに目からウロコ の瞬間だった。 rotはベクトルの微分 今までの電磁気学の数式にも出てきた。 rotが出てきた電磁気の式 rotは「 とベクトル」の外積だ。 回転の意味と言われるが、数式を眺めているだけでは 何も
Incoming Term: rot 回転 なぜ,




0 件のコメント:
コメントを投稿